แนวคิดแรกคือ แคลคูลัสเชิงอนุพันธ์ (Differential Calculus) เป็นทฤษฎีที่ว่าด้วยอัตราการเปลี่ยนแปลง และเกี่ยวข้องกับการหาอนุพันธ์ของฟังก์ชันทางคณิตศาสตร์ ตัวอย่างเช่น การหา ความเร็ว, ความเร่ง หรือความชันของเส้นโค้ง บนจุดที่กำหนดให้. ทฤษฎีของอนุพันธ์หลายส่วนได้แรงบันดาลใจจากปัญหาทางฟิสิกส์
แนวคิดที่สองคือ แคลคูลัสเชิงปริพันธ์ (Integral Calculus) เป็นทฤษฎีที่ได้แรงบันดาลใจจากการคำนวณหาพื้นที่หรือปริมาตรของรูปทรงทางเรขาคณิตต่าง ๆ. ทฤษฎีนี้ใช้กราฟของฟังก์ชันแทนรูปทรงทางเรขาคณิต และใช้ทฤษฎีปริพันธ์ (หรืออินทิเกรต) เป็นหลักในการคำนวณหาพื้นที่และปริมาตร
ทั้งสองแนวคิดที่กำเนิดจากปัญหาที่ต่างกันกลับมีความสัมพันธ์กันลึกซึ้ง โดยทฤษฎีบทมูลฐานของแคลคูลัสกล่าวว่า แท้จริงแล้วทฤษฎีทั้งสองเปรียบเสมือนเป็นด้านทั้งสองของเหรียญอันเดียวกัน นั่นคือเป็นสิ่งเดียวกันเพียงแต่มองคนละมุมเท่านั้น (โดยคร่าว ๆ เรากล่าวได้ว่าอนุพันธ์และปริพันธ์เป็นฟังก์ชันผกผันของ กันและกัน). ในการสอนแคลคูลัสเพื่อความเข้าใจตัวทฤษฎีอย่างลึกซึ้ง ควรกล่าวถึงทั้งสองทฤษฎีและความสัมพันธ์นี้ก่อน แต่การศึกษาในปัจจุบันมักจะกล่าวถึงแคลคูลัสเชิงอนุพันธ์ก่อนเพียงอย่าง เดียว เนื่องจากนำไปใช้งานได้ง่ายกว่า
อนึ่ง การศึกษาแคลคูลัสอย่างละเอียดในเวลาต่อมา ได้ทำให้เกิดศาสตร์ใหม่ ๆ ทางคณิตศาสตร์มากมาย เช่น คณิตวิเคราะห์ และ ทฤษฎีการวัด เป็นต้น
ประวัติ
มีการโต้เถียงกันว่านิวตันหรือไลบ์นิซ ที่เป็นผู้ที่ค้นพบแนวคิดหลักของแคลคูลัสก่อน ความจริงนั้นไม่มีใครรู้ได้ สิ่งที่ยิ่งใหญ่ที่สุด ที่ไลบ์นิซได้พัฒนาให้กับแคลคูลัส คือ เครื่องหมายของเขา เขามักจะใช้เวลาเป็นวัน ๆ นั่งคิดถึงสัญลักษณ์ที่เหมาะสม ที่จะแทนที่แนวคิดทางคณิตศาสตร์ อย่างไรก็ตาม การโต้เถียงกันระหว่างไลบ์นิซ และนิวตัน ได้แบ่งแยกนักคณิตศาสตร์ที่พูดภาษาอังกฤษ ออกจากนักคณิตศาสตร์ในยุโรป เป็นเวลานานหลายปี ซึ่งทำให้คณิตศาสตร์ในอังกฤษล้าหลังกว่ายุโรปเป็นเวลานาน เครื่องหมายที่นิวตันใช้นั้น คล่องตัวน้อยกว่าของไลบ์นิซอย่างเห็นได้ชัด แต่ก็ยังใช้กันในอังกฤษจน Analytical Society ได้ใช้เครื่องหมายของไลบ์นิซในศตวรรษที่ 19 ตอนต้น สันนิษฐานกันว่า นิวตันค้นพบแนวคิดเกี่ยวกับแคลคูลัสก่อน แต่อย่างไรก็ตาม ไลบ์นิซเป็นผู้ที่เผยแพร่ก่อน ทุกวันนี้เป็นที่เชื่อกันว่า ทั้งนิวตันและไลบ์นิซต่างก็ค้นพบแคลคูลัสด้วยตนเองผู้ที่ได้ชื่อว่าเป็นผู้พัฒนาวิชาแคลคูลัสนอกจากนี้คือ เดส์การตส์, Barrow, เดอ แฟร์มาต์, ฮอยเก้นส์ และ วอลลิส โดยเฉพาะ เดอ แฟร์มาต์ ซึ่งบางครั้งได้รับการยกย่องว่าเป็น บิดาแห่งแคลคูลัสเชิงอนุพันธ์. นักคณิตศาสตร์ชาวญี่ปุ่น โควะ เซกิ ซึ่งมีชีวิตอยู่ในช่วงเวลาเดียวกันกับ ไลบ์นิซ และนิวตัน ได้ค้นพบหลักการพื้นฐานบางอย่างเกี่ยวกับ แคลคูลัสเชิงปริพันธ์ แต่เขาไม่เป็นที่รู้จักในโลกตะวันตกในขณะนั้น และเขาก็ไม่ได้ติดต่อกับนักวิชาการชาวตะวันตกเลย
[แก้] แคลคูลัสเชิงอนุพันธ์
อนุพันธ์ (derivative) คือการหาค่าความเปลี่ยนแปลงของตัวแปรหนึ่ง เมื่ออีกตัวแปรหนึ่งเปลี่ยนแปลงในปริมาณที่น้อยมากๆ บางทีอนุพันธ์ที่เราจะได้พบครั้งแรกในโรงเรียนคือ สูตร อัตราเร็ว = ระยะทาง/เวลา สำหรับวัตถุที่เคลื่อนที่ด้วยอัตราเร็วคงที่ อัตราเร็วของคุณซึ่งเป็นอนุพันธ์ที่บอกการเปลี่ยนแปลงตำแหน่งในระยะเวลา หนึ่ง วิชาแคลคูลัสพัฒนาขึ้น เพื่อจัดการกับปัญหาที่ซับซ้อนและเป็นธรรมชาติกว่านี้ ซึ่งอัตราเร็วของคุณอาจเปลี่ยนแปลงได้เมื่อเรากล่าวถึงรายละเอียดแล้ว แคลคูลัสเชิงอนุพันธ์ นิยามอัตราการเปลี่ยนแปลงในขณะใดขณะหนึ่ง (อนุพันธ์) ระหว่างค่าของฟังก์ชัน กับตัวแปรของฟังก์ชัน นิยามจริงๆ ของอนุพันธ์คือ ลิมิตของอัตราส่วนในการเปลี่ยนแปลง (difference quotient). อนุพันธ์คือหัวใจของวิทยาศาสตร์กายภาพ กฎการเคลื่อนที่ของนิวตัน แรง = มวล×ความเร่ง มีความหมายในแคลคูลัส เพราะว่า ความเร่งเป็นอนุพันธ์ค่าหนึ่ง ทฤษฎีแม่เหล็กไฟฟ้าของแมกซ์เวล และทฤษฎีแรงโน้มถ่วงของไอน์สไตน์ (สัมพัทธภาพทั่วไป) นั่นได้กล่าวถึงด้วยภาษาของแคลคูลัสเชิงอนุพันธ์ เช่นเดียวกันกับทฤษฎีพื้นฐานของวงจรไฟฟ้า
อนุพันธ์ของฟังก์ชัน กล่าวถึงกราฟของฟังก์ชันนั้นในช่วงสั้น ๆ ซึ่งทำให้เราสามารถหาจุดสูงสุด และจุดต่ำสุด ของฟังก์ชันได้ เพราะว่าที่จุดเหล่านั้นกราฟจะขนานกับแกนราบ ดิเฟอเรนเชียล แคลคูลัสยังมีการประยุกต์ใช้อื่นๆอีก เช่น ระเบียบวิธีของนิวตัน (Newton's Method) ซึ่งเป็นวิธีในการหาค่ารากของฟังก์ชัน โดยการประมาณค่าโดยเส้นสัมผัส ดังนั้นแคลคูลัสเชิงอนุพันธ์ จึงสามารถนำไปประยุกต์ใช้กับหลากหลายคำถาม ซึ่งถ้ามองแค่ผิวเผินอาจคิดว่า ไม่อาจใช้แคลคูลัสจัดการได้
[แก้] แคลคูลัสเชิงปริพันธ์
แคลคูลัสเชิงปริพันธ์ศึกษาวิธีการหาปริพันธ์ (อินทิกรัล, Integral) ของฟังก์ชัน ซึ่งอาจนิยามจากลิมิตของผลรวมของพจน์ (ซึ่งเรียกว่าลิมิตของผลรวมรีมันน์) แต่ละพจน์นั้นคือพื้นที่ที่เป็นสี่เหลี่ยมผืนผ้าแต่ละแถบใต้กราฟของฟังก์ชัน ทำให้การอินทิเกรตเป็นวิธีที่ได้ผลวิธีหนึ่งในการหาพื้นที่ใต้กราฟ และพื้นที่ผิว และปริมาตรของแข็งเช่นทรงกลมและทรงกระบอก[แก้] พื้นฐานของแคลคูลัส
พื้นฐานที่เคร่งครัดของแคลคูลัส มีฐานมาจาก แนวคิดของฟังก์ชัน และลิมิต มันรวมเทคนิคของพีชคณิตพื้นฐาน และการอุปนัยเชิงคณิตศาสตร์ การศึกษาพื้นฐานของแคลคูลัสสมัยใหม่ รู้จักกันในชื่อ การวิเคราะห์เชิงจริง ซึ่งประกอบด้วย นิยามที่เคร่งครัด และบทพิสูจน์ของทฤษฎีของแคลคูลัส เช่นทฤษฎีการวัด และการวิเคราะห์เชิงฟังก์ชัน[แก้] ทฤษฎีบทมูลฐานของแคลคูลัส เบื้องต้น
ทฤษฎีบทมูลฐานของแคลคูลัสกล่าว ว่า การหาอนุพันธ์และการหาปริพันธ์เป็นวิธีการที่ตรงกันข้ามกัน กล่าวคือ ถ้าเราสร้างฟังก์ชันที่เป็นปริพันธ์ของฟังก์ชันหนึ่งขี้นมา อนุพันธ์ของฟังก์ชันที่เราสร้าง ก็จะเท่ากับฟังก์ชันนั้น นอกจากนี้ เรายังหาปริพันธ์จำกัดเขตได้ด้วยการกำหนดค่าให้กับปฏิยานุพันธ์ทฤษฎีบทมูลฐานของแคลคูลัสเขียนในรูปสัญลักษณ์คณิตศาสตร์ได้ดังนี้: ถ้า f เป็นฟังก์ชันที่มีความต่อเนื่องบนช่วง [a, b] และ F เป็นปฏิยานุพันธ์ของ f บนช่วง [a, b] แล้ว
- และสำหรับทุก x ในช่วง [a, b] จะได้ว่า
[แก้] การประยุกต์นำมาใช้
การพัฒนาและการใช้แคลคูลัสได้ขยายผลไปแทบทุกส่วนของการใช้ชีวิตในยุคใหม่ มันเป็นพื้นฐานของวิทยาศาสตร์เกือบทุกสาขาโดยเฉพาะ ฟิสิกส์ การพัฒนาสมัยใหม่เกือบทั้งหมด เช่น เทคนิคการก่อสร้าง การบิน และเทคโนโลยีอื่น ๆ เกือบทั้งหมด มีพื้นฐานมาจากแคลคูลัสแคลคูลัสได้ขยายไปสู่ สมการเชิงอนุพันธ์ แคลคูลัสเวกเตอร์ แคลคูลัสของการเปลี่ยนแปลง การวิเคราะห์เชิงซ้อน แคลคูลัสเชิงเวลา แคลคูลัสกณิกนันต์ และ ทอพอโลยีเชิงอนุพันธ์
ทฤษฎีบทมูลฐานของแคลคูลัส กล่าวว่าอนุพันธ์ และปริพันธ์ ซึ่งเป็นการดำเนินการหลักในแคลคูลัสนั้นผกผันกัน ซึ่งหมายความว่าถ้านำฟังก์ชันต่อเนื่องใดๆ มาหาปริพันธ์ แล้วนำมาหาอนุพันธ์ เราจะได้ฟังก์ชันเดิม ทฤษฎีบทนี้เหมือนว่าเป็นหัวใจสำคัญของแคลคูลัสที่นับได้ว่าเป็นทฤษฎีบท มูลฐานของทั้งสาขานี้ ผลต่อเนื่องที่สำคัญของทฤษฎีบทนี้ ซึ่งบางทีเรียกว่าทฤษฎีบทมูลฐานของแคลคูลัสบทที่สองนั้นทำให้เราสามารถคำนวณ หาปริพันธ์โดยใช้ปฏิยานุพันธ์ ของฟังก์ชัน
ภาพโดยทั่วไป
โดยทั่วไปแล้ว ทฤษฎีบทนี้กล่าวว่าผลรวมของการเปลี่ยนแปลงที่น้อยยิ่ง ในปริมาณในช่วงเวลา (หรือปริมาณอื่นๆ) นั้นเข้าใกล้การเปลี่ยนแปลงรวมเพื่อให้เห็นด้วยกับข้อความนี้ เราจะเริ่มด้วยตัวอย่างนี้ สมมติว่าอนุภาคเดินทางบนเส้นตรงโดยมีตำแหน่งจากฟังก์ชัน x(t) เมื่อ t คือเวลา อนุพันธ์ของฟังก์ชันนี้เท่ากับความเปลี่ยนแปลงที่น้อยมากๆของ x ต่อช่วงเวลาที่น้อยมากๆ (แน่นอนว่าอนุพันธ์ต้องขึ้นอยู่กับเวลา) เรานิยามความเปลี่ยนแปลงของระยะทางต่อช่วงเวลาว่าเป็นอัตราเร็ว v ของอนุภาค ด้วยสัญกรณ์ของไลบ์นิซ
[แก้] เนื้อหาของทฤษฎีบท
ทฤษฎีบทนี้ว่าไว้ว่าให้ f เป็นฟังก์ชันต่อเนื่องบนช่วง [a, b] ถ้า F เป็นฟังก์ชันที่นิยามสำหรับ x ที่อยู่ใน [a, b] ว่า
ให้ f เป็นฟังก์ชันต่อเนื่องบนช่วง [a, b] ถ้า F เป็นฟังก์ชันที่
 สำหรับทุก x ที่อยู่ใน [a, b]
สำหรับทุก x ที่อยู่ใน [a, b]
[แก้] ผลที่ตามมา
ให้ f เป็นฟังก์ชันที่มีความต่อเนื่องบนช่วง [a, b]. ถ้า F เป็นฟังก์ชันที่ สำหรับทุก x ที่อยู่ใน [a, b]
สำหรับทุก x ที่อยู่ใน [a, b]
[แก้] บทพิสูจน์
[แก้] ส่วนที่ 1
กำหนดให้
- (ผลรวมพื้นที่ของบริเวณที่อยู่ติดกัน จะเท่ากับ พื้นที่ของบริเวณทั้งสองรวมกัน)
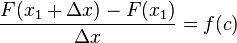
- สังเกตว่าสมการข้างซ้าย คือ อัตราส่วนเชิงผลต่างของนิวตัน (Newton's difference quotient) ของ F ที่ x1
จาก
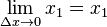 และ
และ 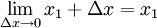
ตามทฤษฎีบท squeeze จะได้ว่า
(Leithold et al, 1996)
[แก้] ส่วนที่ 2
ต่อไปนี้คือบทพิสูจน์ลิมิตโดย ผลรวมของรีมันน์-ดาบูต์ให้ f เป็นฟังก์ชันที่มีความต่อเนื่องบนช่วง [a, b] และ F เป็นปฏิยานุพันธ์ของ f พิจารณานิพจน์ต่อไปนี้
 จะได้
จะได้ให้ f เป็นฟังก์ชันที่มีความต่อเนื่องบนช่วง [a, b] และมีอนุพันธ์บนช่วง (a, b) แล้ว จะมี c อยู่ใน (a, b) ที่ทำให้
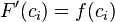 และ xi − xi − 1 สามารถเขียนในรูป Δx ของผลแบ่งกั้น i
และ xi − xi − 1 สามารถเขียนในรูป Δx ของผลแบ่งกั้น iโดยการหาลิมิตของนิพจน์นี้เป็นเมื่อค่าเฉลี่ยของส่วนต่างๆนี้ เข้าใกล้ศูนย์ เราจะได้ ปริพันธ์แบบรีมันน์ นั่นคือ เราหาลิมิตเมื่อขนาดส่วนที่ใหญ่ที่สุดเข้าใกล้ศูนย์ จะได้ส่วนอื่นๆมีขนาดเล็กลง และจำนวนส่วนเข้าใกล้อนันต์
ดังนั้น เราจะใส่ลิมิตไปทั้งสองข้างของสมการ (2) จะได้
[แก้] ตัวอย่าง
ตัวอย่างเช่น ถ้าคุณต้องการคำนวณหา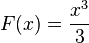 เป็นปฏิยานุพันธ์ ดังนั้น
เป็นปฏิยานุพันธ์ ดังนั้นจะได้
![\int_1^3 \frac{dx}{x}=\big[\ln|x|\big]_1^3 =\ln 3-\ln1=\ln 3](http://upload.wikimedia.org/math/e/e/b/eeb3b0f6a30e7c80bac92f30898eb11a.png)
[แก้] นัยทั่วไป
เราไม่จำเป็นต้องให้ f ต่อเนื่องตลอดทั้งช่วง ดังนั้นส่วนที่ 1 ของทฤษฎีบทจะกล่าวว่า ถ้า f เป็นฟังก์ชันที่สามารถหาปริพันธ์เลอเบกบนช่วง [a,b] และ x0 เป็นจำนวนในช่วง [a,b] ซึ่ง f ต่อเนื่องที่ x0 จะได้ส่วนที่ 2ของทฤษฎีบทนี้เป็นจริงสำหรับทุกฟังก์ชัน f ที่สามารถหาปริพันธ์เลอเบกได้ และมีปฏิยานุพันธ์ F (ไม่ใช่ทุกฟังก์ชันที่หาอนุพันธ์ได้)
ส่วนของทฤษฎีบทของเทย์เลอร์ซึ่งกล่าวถึงพจน์ที่เกิดข้อผิดพลาดเป็นปริพันธ์สามารถมองได้เป็นนัยทั่วไปของทฤษฎีบทมูลฐานของแคลคูลัส
มีทฤษฎีบทหนึ่งสำหรับฟังก์ชันเชิงซ้อน: ให้ U เป็นเซตเปิดใน
 และ
และ 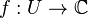 เป็นฟังก์ชันที่มี ปริพันธ์โฮโลมอร์ฟ F ใน U ดังนั้นสำหรับเส้นโค้ง
เป็นฟังก์ชันที่มี ปริพันธ์โฮโลมอร์ฟ F ใน U ดังนั้นสำหรับเส้นโค้ง ![\gamma : [a,b] \to U](http://upload.wikimedia.org/math/9/0/7/9078483f387058616c5c969450185a37.png) ปริพันธ์เส้นโค้งจะคำนวณได้จาก
ปริพันธ์เส้นโค้งจะคำนวณได้จากใน คณิตศาสตร์ ฟังก์ชัน คือ ความสัมพันธ์ จาก เซต หนึ่ง (โดเมน) ไปยังอีกเซตหนึ่ง (โคโดเมน ไม่ใช่ เรนจ์) โดยที่สมาชิกตัวหน้าไม่ซ้ำกัน ความคิดรวบยอดของฟังก์ชันนี้เป็นพื้นฐานของทุกสาขาของคณิตศาสตร์และวิทยาศาสตร์เชิงปริมาณ
แนวคิด
แนวคิดที่สำคัญที่สุดคือ ฟังก์ชันนั้นเป็น "กฎ" ที่กำหนด ผลลัพธ์โดยขึ้นกับสิ่งที่นำเข้ามา ต่อไปนี้เป็นตัวอย่าง- แต่ละคนจะมีสีที่ตนชอบ (แดง, ส้ม, เหลือง, เขียว, ฟ้า, น้ำเงิน, คราม หรือม่วง) สีที่ชอบเป็นฟังก์ชันของแต่ละคน เช่น จอห์นชอบสีแดง แต่คิมชอบสีม่วง ในที่นี้สิ่งที่นำเข้าคือคน และผลลัพธ์คือ 1 ใน 8 สีดังกล่าว
- มีเด็กบางคนขายน้ำมะนาวในช่วงฤดูร้อน จำนวนน้ำมะนาวที่ขายได้เป็นฟังก์ชันของอุณหภูมิภายนอก ตัวอย่างเช่น ถ้าภายนอกมีอุณหภูมิ 85 องศา จะขายได้ 10 แก้ว แต่ถ้าอุณหภูมิ 95 องศา จะขายได้ 25 แก้ว ในที่นี้ สิ่งที่นำเข้าคืออุณหภูมิ และผลลัพธ์คือจำนวนน้ำมะนาวที่ขายได้
- ก้อนหินก้อนหนึ่งปล่อยลงมาจากชั้นต่างๆของตึกสูง ถ้าปล่อยจากชั้นที่สอง จะใช้เวลา 2 วินาที และถ้าปล่อยจากชั้นที่แปด จะใช้เวลา (เพียง) 4 วินาที ในที่นี้ สิ่งนำเข้าคือชั้น และผลลัพธ์คือระยะเวลาเป็นวินาที ฟังก์ชันนี้อธิบายความสัมพันธ์ระหว่าง เวลาที่ก้อนหินใช้ตกถึงพื้นกับชั้นที่มันถูกปล่อยลงมา (ดู ความเร่ง)
ชนิดของฟังก์ชันธรรมดาเกิดจากที่ทั้งอาร์กิวเมนต์และค่าของฟังก์ชันเป็น ตัวเลขทั้งคู่ ความสัมพันธ์ของฟังก์ชันมักจะเขียนในรูปสูตร และจะได้ค่าของฟังก์ชันมาทันทีเพียงแทนที่อาร์กิวเมนต์ลงในสูตร เช่น
- f(x) = x2
โดยนัยทั่วไปแล้ว ฟังก์ชันจะสามารถมีได้มากกว่าหนึ่งอาร์กิวเมนต์ เช่น
- g(x,y) = xy
ในวิทยาศาสตร์ เรามักจะต้องเผชิญหน้ากับฟังก์ชันที่ไม่ได้กำหนดขึ้นจากสูตร เช่นอุณหภูมิบนพื้นผิวโลกในเวลาใดเวลาหนึ่ง นี่เป็นฟังก์ชันที่มีสถานที่และเวลาเป็นอาร์กิวเมนต์ และให้ผลลัพธ์เป็นอุณหภูมิของสถานที่และเวลานั้นๆ
เราได้เห็นแล้วว่าแนวคิดของฟังก์ชันไม่ได้จำกัดอยู่แค่การคำนวณด้วยตัว เลขเท่านั้น และไม่ได้จำกัดอยู่แค่การคำนวณด้วย แนวคิดของคณิตศาสตร์เกี่ยวกับฟังก์ชัน เป็นแนวคิดโดยทั่วไปและไม่ได้จำกัดอยู่แค่สถานการณ์ที่เกี่ยวข้องกับตัวเลข เท่านั้น แน่นอนว่าฟังก์ชันเชื่อมโยง "โดเมน" (เซตของสิ่งนำเข้า) เข้ากับ "โคโดเมน" (เซตของผลลัพธ์ที่เป็นไปได้) ดังนั้นสมาชิกแต่ละตัวของโดเมนจะจับคู่กับสมาชิกตัวใดตัวหนึ่งของโคโดเมน เท่านั้น ฟังก์ชันนั้นนิยามเป็นความสัมพันธ์ที่แน่นอน ดังที่จะกล่าวต่อไป เป็นเหตุจากลักษณะทั่วไปนี้ แนวคิดรวบยอดของฟังก์ชันจึงเป็นพื้นฐานของทุกสาขาในคณิตศาสตร์
[แก้] ประวัติ
ในทางคณิตศาสตร์ "ฟังก์ชัน" บัญญัติขึ้นโดย ไลบ์นิซ ใน พ.ศ. 2237 เพื่ออธิบายปริมาณที่เกี่ยวข้องกับเส้นโค้ง เช่น ความชันของเส้นโค้ง หรือจุดบน เส้นโค้ง ฟังก์ชันที่ไลบ์นิซพิจารณานั้นในปัจจุบันเรียกว่า ฟังก์ชันที่หาอนุพันธ์ได้ และเป็นชนิดของฟังก์ชันที่มักจะแก้ด้วยผู้ที่ไม่ใช่นักคณิตศาสตร์ สำหรับฟังก์ชันชนิดนี้ เราสามารถพูดถึงลิมิตและอนุพันธ์ ซึ่งเป็นการทฤษฎีเซต พวกเขาได้พยายามนิยามวัตถุทางคณิตศาสตร์ทั้งหมดด้วย เซต ดีริคเลท และ โลบาเชฟสกี ได้ให้นิยามสมัยใหม่ของฟังก์ชันออกมาเกือบพร้อมๆกันในคำนิยามนี้ ฟังก์ชันเป็นเพียงกรณีพิเศษของความสัมพันธ์ อย่างไรก็ตาม เป็นกรณีที่มีความน่าสนใจเป็นพิเศษ ความแตกต่างระหว่างคำนิยามสมัยใหม่กับคำนิยามของออยเลอร์นั้นเล็กน้อยมาก
แนวคิดของ ฟังก์ชัน ที่เป็นกฎในการคำนวณ แทนที่เป็นความสัมพันธ์ชนิดพิเศษนั้น อยู่ในคณิตตรรกศาสตร์ และวิทยาการคอมพิวเตอร์เชิงทฤษฎี ด้วยหลายระบบ รวมไปถึง แคลคูลัสแลมบ์ดา ทฤษฎีฟังก์ชันเวียนเกิด และเครื่องจักรทัวริง
[แก้] นิยามอย่างเป็นทางการ
ฟังก์ชัน f จากข้อมูลนำเข้าในเซต X ไปยังผลที่เป็นไปได้ในเซต Y (เขียนเป็น ) คือความสัมพันธ์ ระหว่าง X กับ Y ซึ่ง
) คือความสัมพันธ์ ระหว่าง X กับ Y ซึ่ง- สำหรับทุกค่า x ใน X จะมี y ใน Y ซึ่ง x f y (x มีความสัมพันธ์ f กับ y) นั่นคือ สำหรับค่านำเข้าแต่ละค่า จะมีผลลัพธ์ใน Y อย่างน้อย 1 ผลลัพธ์เสมอ
- ถ้า x f y และ x f z แล้ว y = z นั่นคือ ค่านำเข้าหลายค่าสามารถมีผลลัพธ์ได้ค่าเดียว แต่ค่านำเข้าค่าเดียวไม่สามารถมีผลลัพธ์หลายผลลัพธ์ได้
จากนิยามข้างต้น เราสามารถเขียนอย่างสั้นๆได้ว่า ฟังก์ชันจาก X ไปยัง Y คือเซตย่อย f ของผลคูณคาร์ทีเซียน
 โดยที่แต่ละค่าของ x ใน X จะมี y ใน Y ที่แตกต่างกัน โดยที่คู่อันดับ (x, y) อยู่ใน f
โดยที่แต่ละค่าของ x ใน X จะมี y ใน Y ที่แตกต่างกัน โดยที่คู่อันดับ (x, y) อยู่ใน fเซตของฟังก์ชัน
 ทุกฟังก์ชันแทนด้วย YX สังเกตว่า |YX| = |Y||X| (อ้างถึง จำนวนเชิงการนับ)
ทุกฟังก์ชันแทนด้วย YX สังเกตว่า |YX| = |Y||X| (อ้างถึง จำนวนเชิงการนับ)ความสัมพันธ์ระหว่าง X กับ Y ซึ่งเป็นไปตามเงื่อนไข (1) นั่นคือฟังก์ชันหลายค่า ฟังก์ชันทุกฟังก์ชันเป็นฟังก์ชันหลายค่า แต่ฟังก์ชันหลายค่าไม่ทุกฟังก์ชันเป็นฟังก์ชัน ความสัมพันธ์ระหว่าง X กับ Y ซึ่งเป็นไปตามเงื่อนไข (2) นั่นคือฟังก์ชันบางส่วน ฟังก์ชันทุกฟังก์ชันเป็นฟังก์ชันบางส่วน แต่ฟังก์ชันบางส่วนไม่ทุกฟังก์ชันเป็นฟังก์ชัน "ฟังก์ชัน" คือความสัมพันธ์ที่เป็นไปตามเงื่อนไขทั้งสองเงื่อนไข
ดูตัวอย่างต่อไปนี้
 สมาชิก 3 ใน X สัมพันธ์กับ b และ c ใน Y ความสัมพันธ์นี้เป็นฟังก์ชันหลายค่า แต่ไม่เป็นฟังก์ชัน
สมาชิก 3 ใน X สัมพันธ์กับ b และ c ใน Y ความสัมพันธ์นี้เป็นฟังก์ชันหลายค่า แต่ไม่เป็นฟังก์ชัน สมาชิก 1 ใน X ไม่สัมพันธ์กับสมาชิกใดๆเลยใน Y ความสัมพันธ์นี้เป็นฟังก์ชันบางส่วน แต่ไม่เป็นฟังก์ชัน
สมาชิก 1 ใน X ไม่สัมพันธ์กับสมาชิกใดๆเลยใน Y ความสัมพันธ์นี้เป็นฟังก์ชันบางส่วน แต่ไม่เป็นฟังก์ชัน ความสัมพันธ์นี้เป็นฟังก์ชันจาก X ไปยัง Y เราสามารถหานิยามฟังก์ชันนี้อย่างชัดแจ้งได้เป็น f={ (1,d) , (2,d) , (3,c) } หรือเป็น
ความสัมพันธ์นี้เป็นฟังก์ชันจาก X ไปยัง Y เราสามารถหานิยามฟังก์ชันนี้อย่างชัดแจ้งได้เป็น f={ (1,d) , (2,d) , (3,c) } หรือเป็น[แก้] โดเมน, โคโดเมน และเรนจ์
X ซึ่งคือเซตข้อมูลนำเข้าเรียกว่า โดเมนของ f และ Y ซึ่งคือเซตของผลลัพธ์ที่เป็นไปได้ เรียกว่า โคโดเมน เรนจ์ของ f คือเซตของผลลัพธ์จริงๆ {f (x) : x ในโดเมน} ระวังว่าบางครั้งโคโดเมนจะถูกเรียกว่าเรนจ์ เนื่องจากความผิดพลาดจากการจำแนกระหว่างผลที่เป็นไปได้กับผลจริงๆฟังก์ชันนั้นเรียกชื่อตามเรนจ์ของมัน เช่น ฟังก์ชันจำนวนจริง หรือ ฟังก์ชันจำนวนเชิงซ้อน
เอนโดฟังก์ชัน คือฟังก์ชันที่โดเมนและเรนจ์เป็นเซตเดียวกัน
ในสาขาวิทยาการคอมพิวเตอร์ แบบชนิดข้อมูลของอาร์กิวเมนต์และค่าที่คืนกลับมาระบุโดเมนและโคโดเมน (ตามลำดับ) ของโปรแกรมย่อย ดังนั้นโดเมนและโคโดเมนจะถูกกำหนดไว้ในแต่ละฟังก์ชัน แต่เรนจ์จะเกี่ยวกับว่าค่าที่คืนกลับมาจะเป็นอย่างไร
[แก้] ฟังก์ชันหนึ่งต่อหนึ่ง ฟังก์ชันทั่วถึง และฟังก์ชันหนึ่งต่อหนึ่งทั่วถึง
เราสามารถแบ่งฟังก์ชันตามลักษณะความสัมพันธ์ได้ดังนี้- ฟังก์ชันหนึ่งต่อหนึ่ง (1-1) ฟังก์ชันจะคืนค่าที่ไม่เหมือนกันหากนำเข้าค่าคนละค่ากัน กล่าวคือ ถ้า x1 และ x2 เป็นสมาชิกของโดเมนของ f แล้ว f (x1) = f (x2) ก็ต่อเมื่อ x1 = x2
- ฟังก์ชันทั่วถึง (แบบ onto) ฟังก์ชันจะมีเรนจ์เท่ากับโคโดเมน กล่าวคือ ถ้า y เป็นสมาชิกใดๆของโคโดเมนของ f แล้วจะมี x อย่างน้อย 1 ตัว ซึ่ง f (x) = y
- ฟังก์ชันหนึ่งต่อหนึ่งทั่วถึง เป็นฟังก์ชันที่เป็นทั้งฟังก์ชันหนึ่งต่อหนึ่ง และฟังก์ชันทั่วถึง มักจะใช้แสดงว่าเซต X และเซต Y มีขนาดเท่ากัน
[แก้] ภาพ และบุพภาพ
ภาพ (image) ของสมาชิก x ∈ X ภายใต้ f คือผลลัพธ์ f (x)ภาพของเซตย่อย A⊂X ภายใต้ f คือเซตย่อย Y ซึ่งมีนิยามดังนี้
- f[A] = {f (x) | x อยู่ใน A}
สังเกตว่าเรนจ์ของ f คือภาพ f (X) ของโดเมนของมัน. ในฟังก์ชันข้างบน ภาพของ {2, 3} ภายใต้ f คือ f ({2, 3}) = {c, d} และเรนจ์ของ f คือ {c, d}
บุพภาพ (preimage) (หรือ ภาพผกผัน) ของเซต B ⊂ Y ภายใต้ f คือเซตย่อยของ X ซึ่งมีนิยามคือ
- f −1 (B) = {x อยู่ใน X | f (x) ∈B}
[แก้] กราฟของฟังก์ชัน
กราฟของฟังก์ชัน f คือเซตของคู่อันดับ (x, f (x)) ทั้งหมด สำหรับค่า x ทั้งหมดในโดเมน X มีทฤษฎีบทที่แสดงหรือพิสูจน์ง่ายมากเมื่อใช้กราฟ เช่น ทฤษฎีบทกราฟปิด ถ้า X และ Y เป็นเส้นจำนวนจริง แล้วนิยามนี้จะสอดคล้องกับแนวคิดของกราฟสังเกตว่าเมื่อความสัมพันธ์ระหว่างสองเซต X และ Y มักจะแสดงด้วยเซตย่อยของ X×Y นิยามอย่างเป็นทางการของฟังก์ชันนั้นระบุฟังก์ชัน f ด้วยกราฟของมัน
[แก้] ตัวอย่างฟังก์ชัน
- ความสัมพันธ์ wght ระหว่างบุคคลกับน้ำหนักในเวลาใดเวลาหนึ่ง
- ความสัมพันธ์ cap ระหว่างประเทศกับเมืองหลวงของประเทศนั้น
- ความสัมพันธ์ sqr ระหว่างจำนวนธรรมชาติ n กับกำลังสอง n2
- ความสัมพันธ์ ln ระหว่างจำนวนจริงบวก x กับลอการิทึมฐานธรรมชาติ ln (x) แต่ความสัมพันธ์ระหว่างจำนวนจริงกับลอการิทึมฐานธรรมชาตินั้นไม่เป็น ฟังก์ชัน เพราะว่าจำนวนจริงทุกจำนวนไม่ได้มีลอการิทึมฐานธรรมชาติ นั่นคือเป็นความสัมพันธ์ไม่ทั้งหมด
- ความสัมพันธ์ dist ระหว่างจุดบนระนาบ R2 กับระยะทางจากจุดกำเนิด (0,0)
[แก้] คุณสมบัติของฟังก์ชัน
ฟังก์ชันอาจเป็น- ฟังก์ชันคู่หรือคี่
- ฟังก์ชันต่อเนื่องหรือไม่ต่อเนื่อง
- ฟังก์ชันจำนวนจริง หรือ ฟังก์ชันเชิงซ้อน
- ฟังก์ชันสเกลาร์ หรือ ฟังก์ชันเวกเตอร์
[แก้] ฟังก์ชันแบบ n-ary : ฟังก์ชันหลายตัวแปร
ฟังก์ชันที่เราใช้ส่วนมักจะเป็น ฟังก์ชันหลายตัวแปร ค่าที่ได้จะขึ้นอยู่กับปัจจัยต่างๆกัน จากมุมมองของคณิตศาสตร์ ตัวแปรทั้งหมดต้องแสดงอย่างชัดแจ้งเพื่อที่จะเกิดความสัมพันธ์แบบฟังก์ชัน - ไม่มีปัจจัย "ซ่อนเร้น" อยู่ และเช่นกัน จากมุมมองของคณิตศาสตร์ ไม่มีความแตกต่างเชิงคุณภาพระหว่างฟังก์ชันตัวแปรเดียวกับฟังก์ชันหลายตัว แปร ฟังก์ชันสามตัวแปรจำนวนจริงนั้นก็คือฟังก์ชันของ triple ((x,y,z)) ของจำนวนจริงถ้าโดเมนของฟังก์ชันหนึ่งเป็นเซตย่อยของ ผลคูณคาร์ทีเซียน ของ n เซต แล้ว เราเรียกฟังก์ชันนี้ว่า ฟังก์ชัน n-ary ตัวอย่างเช่นฟังก์ชัน dist มีโดเมน
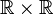 จึงเป็นฟังก์ชันทวิภาค ในกรณีนี้ dist ((x,y)) เขียนอย่างง่ายเป็น dist (x,y)
จึงเป็นฟังก์ชันทวิภาค ในกรณีนี้ dist ((x,y)) เขียนอย่างง่ายเป็น dist (x,y)การดำเนินการ ก็เป็นฟังก์ชันหลายตัวแปรชนิดหนึ่ง ในพีชคณิตนามธรรม ตัวดำเนินการเช่น "*" นั้นนิยามจากฟังก์ชันทวิภาค เมื่อเราเขียนสูตรเช่น x*y ในสาขานี้ เสมือนกับว่าเราเรียกใช้ฟังก์ชัน * (x,y) โดยปริยาย เพียงแต่เขียนในรูปสัญกรณ์เติมกลาง (infix notation) ซึ่งสะดวกกว่า
ตัวอย่างที่สำคัญทางทฤษฎีตัวอย่างหนึ่งคือ กำหนดการเชิงฟังก์ชัน ซึ่งใช้แนวคิดของฟังก์ชันเป็นศูนย์กลาง ด้วยวิธีนี้ การจัดการฟังก์ชันหลายตัวแปรทำได้เหมือนเป็นการดำเนินการ ซึ่งแคลคูลัสแลมบ์ดา มีวากยสัมพันธ์ (syntax) ให้เรา
[แก้] การประกอบฟังก์ชัน
ฟังก์ชัน f: Xye → Y และ g:Y → Z สามารถประกอบกันได้ ซึ่งจะได้ผลเป็นฟังก์ชันประกอบ g o f: X → Z ซึ่งมีนิยามคือ (g o f) (x) = g (f (x)) สำหรับทุกค่าของ x ใน X ตัวอย่างเช่น สมมติว่าความสูงของเครื่องบินที่เวลา t เป็นไปตามฟังก์ชัน h (t) และความเข้มข้นของออกซิเจนในอากาศที่ความสูง x เป็นไปตามฟังก์ชัน c (x) ดังนี้น (c o h) (t) จะบอกความเข้มข้นของออกซิเจนในอากาศรอบๆเครื่องบินที่เวลา t[แก้] ฟังก์ชันผกผัน
ถ้าฟังก์ชัน f: X → Y เป็นฟังก์ชันหนึ่งต่อหนึ่งต่อเนื่อง แล้ว พรีอิเมจของสมาชิก y ใดๆในโคโดเมน Y จะเป็นเซตโทน ฟังก์ชันจาก y ∈ Y ไปยังพรีอิเมจ f −1 (y) ของมัน คือฟังก์ชันที่เรียกว่า ฟังก์ชันผกผัน ของ f เขียนแทนด้วย f −1ตัวอย่างหนึ่งของฟังก์ชันผกผันสำหรับ f (x) = 2x คือ f −1 (x) = x/2 ฟังก์ชันผกผันคือฟังก์ชันที่ย้อนการกระทำของฟังก์ชันต้นแบบของมัน ดู อิเมจผกผัน
บางครั้งฟังก์ชันผกผันก็หายากหรือไม่มี พิจารณา f(x) = x2 ฟังก์ชัน
 ไม่ใช่ฟังก์ชันผกผันเมื่อโดเมนของ f คือ
ไม่ใช่ฟังก์ชันผกผันเมื่อโดเมนของ f คือ 
ในวิชาคณิตศาสตร์ ลิมิตของฟังก์ชัน เป็นแนวคิดพื้นฐานของ คณิตวิเคราะห์ (ภาคทฤษฎีของแคลคูลัส)
ถ้าเราพูดว่า ฟังก์ชัน f มีลิมิต L ที่จุด p หมายความว่า ผลลัพธ์ของ f จะเข้าใกล้ L ที่จุดใกล้จุด p สำหรับนิยามอย่างเป็นทางการนั้น มีการกำหนดขึ้นครั้งแรก ช่วงปลายของคริสต์ศตวรรษที่ 19 มีรายละเอียดอยู่ข้างล่าง
ประวัติ
ดูที่ คณิตวิเคราะห์[แก้] นิยามเป็นทางการ
[แก้] ฟังก์ชันบนปริภูมิอิงระยะทาง
กำหนดให้ f : (M,dM) -> (N,dN) เป็นการส่งค่าระหว่าง (เป็นฟังก์ชันที่นิยามบน) ปริภูมิอิงระยะทาง สองปริภูมิ, และกำหนดให้ p ∈M และ L ∈N, เราจะกล่าวว่า "ลิมิตของ f ที่ p คือ L" และเขียนว่าจะมี
δ > 0 ที่ สำหรับทุกๆ x ∈M และ dM(x, p) < δ แล้ว, dN(f(x), L) < ε
[แก้] ฟังก์ชันค่าจริง
เซตของจำนวนจริงหรือเส้นจำนวนจริง โดยทั่วไปสามารถมองเป็นปริภูมิอิงระยะทางได้ โดยมี d(x,y): = | x − y | . เช่นเดียวกับ เส้นจำนวนจริงขยาย (เส้นจำนวนจริงที่เพิ่ม +∞ และ -∞ เข้าไปด้วย) ก็สามารถมองเป็นปริภูมิอิงระยะทางได้ โดยมี d(x,y): = | arctan(x) − arctan(y) |[แก้] ลิมิตของฟังก์ชันค่าจริงที่จุดใดจุดหนึ่ง
ให้ f เป็นฟังก์ชันค่าจริง แล้วเราจะเขียนซึ่งเป็นกรณีพิเศษของฟังก์ชันบนปริภูมิอิงระยะทาง ที่มีทั้ง M และ N เป็นเซตของจำนวนจริง และ d(x,y) = |x-y|.ก็ต่อเมื่อ สำหรับทุกค่าของ ε > 0 (ไม่ว่าจะเล็กเท่าใด) จะต้องมี δ > 0 อย่างน้อยหนึ่งค่า ที่ สำหรับทุกค่าของจำนวนจริง x ที่ 0 < |x-p| < δ, |f(x)-L| < ε
หรือเราจะเขียน
หรือจะเขียนว่าก็ต่อเมื่อ สำหรับทุกค่าของ R > 0 (ไม่ว่าจะใหญ่เท่าใด) จะต้องมี δ > 0 อย่างน้อยหนึ่งค่า ที่ สำหรับทุกค่าของจำนวนจริง x ที่ 0 < |x-p| < δ, f(x) > R;
ถ้าในนิยาม เราใช้ x-p แทน |x-p| เราก็จะได้ ลิมิตขวา เขียนแทนโดย :ก็ต่อเมื่อ สำหรับทุกค่าของ R < 0 จะต้องมี δ > 0 อย่างน้อยหนึ่งค่า ที่ สำหรับทุกค่าของจำนวนจริง x ที่ 0 < |x-p| < δ, f(x) < R.
 และถ้าใช้ p-x แทน ก็จะได้ ลิมิตซ้าย เขียนแทนโดย :
และถ้าใช้ p-x แทน ก็จะได้ ลิมิตซ้าย เขียนแทนโดย :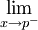
[แก้] ลิมิตของฟังก์ชันค่าจริง ณ อนันต์
ให้ f(x) เป็นฟังก์ชันค่าจริง เราจะพิจารณาลิมิตของฟังก์ชันเมื่อ x เพิ่มขึ้น หรือลดลงอย่างไม่มีที่สิ้นสุด
เราจะเขียน
[แก้] ฟังก์ชันค่าเชิงซ้อน
ระนาบเชิงซ้อน ที่มีตัววัด (metric) เป็น d(x,y): = | x − y | จะเป็นปริภูมิอิงระยะทาง (metric space) ด้วยเช่นกัน จะมีลิมิตสองประเภทเมื่อเราพูดถึงฟังก์ชันค่าเชิงซ้อน[แก้] ลิมิตของฟังก์ชันที่จุดใดจุดหนึ่ง
สมมติให้ f เป็นฟังก์ชันค่าเชิงซ้อน แล้วเราจะเขียนว่า- สำหรับ ε > 0 ใดๆ จะมี δ >0 อย่างน้อย 1 ค่า ซึ่งสำหรับจำนวนจริง x ใดๆ ซึ่ง 0<|x-p|<δ จะได้ |f(x)-L|<ε
[แก้] ลิมิตของฟังก์ชัน ณ อนันต์
เราจะเขียน- สำหรับ ε > 0 ใดๆ จะมี S >0 ซึ่งสำหรับจำนวนเชิงซ้อน |x|>S ใดๆ เราจะได้ |f(x)-L|<ε
[แก้] ตัวอย่าง
[แก้] ฟังก์ชันค่าจริง
 | ลิมิตของ x2 เมื่อ x เข้าใกล้ 3 คือ 9 ในกรณีนี้ ฟังก์ชันนั้นต่อเนื่อง และค่าของมันมีนิยามที่จุดนั้น ค่าลิมิตจึงเท่ากับการแทนค่าฟังก์ชัน |
 | ลิมิตของ xx เมื่อ x เข้าใกล้ 0 จากทางขวาคือ 1 |
  | ลิมิตสองด้านของ 1/x เมื่อ x เข้าใกล้ 0 นั้นไม่มีนิยาม ลิมิตของ 1/x เมื่อ x เข้าใกล้ 0 จากทางขวาคือ +∞ |
  | ลิมิตด้านเดียวของ |x|/x เมื่อ x เข้าใกล้ 0 คือ 1 จากด้านบวกและคือ -1 จากด้านลบ สังเกตว่า |x|/x = -1 เมื่อ x เป็นลบ และ |x|/x = 1 เมื่อ x เป็นบวก |
 | ลิมิตของ x sin(1/x) เมื่อ x เข้าใกล้ 0 คือ 0 |
 | ฟังก์ชันยกกำลังที่มีเลขชี้กำลังเป็นลบใดๆ เข้าใกล้ 0 เมื่อขนาดของ x เพิ่มขึ้นเรื่อยๆ อย่างไม่มีขอบเขตจำกัด |
 | ฟังก์ชันยกกำลังใดๆ จะมีขนาดลดลงเป็นศูนย์ เทียบกับฟังก์ชันเลขชี้กำลังเพิ่มใดๆ เมื่อ x เพิ่มขึ้นเรื่อยๆ อย่างไม่มีขอบเขตจำกัด |
 | ฟังก์ชันลอการิทึมใดๆ จะมีขนาดลดลงเป็นศูนย์ เทียบกับฟังก์ชันยกกำลังที่เป็นบวกใดๆ เมื่อ x เพิ่มขึ้นเรื่อยๆ อย่างไม่มีขอบเขตจำกัด |
 | ฟังก์ชันเลขชี้กำลังใดๆ จะมีขนาดลดลงเป็นศูนย์ เทียบกับฟังก์ชันแฟกทอเรียลใดๆ เมื่อ x เพิ่มขึ้นเรื่อยๆ อย่างไม่มีขอบเขตจำกัด |
[แก้] ฟังก์ชันบนปริภูมิอิงระยะทาง
- ถ้า z เป็นจำนวนเชิงซ้อน โดยที่ |z| < 1 แล้วลำดับ z, z2, z3, ... ของจำนวนเชิงซ้อนจะลู่เข้าโดยมีลิมิตเป็น 0 โดยเรขาคณิตแล้ว จำนวนเหล่านี้จะ "เวียนเป็นก้นหอย" เข้าสู่จุดกำเนิด ตามเส้นก้นหอยลอการิทึม
- ในปริภูมิอิงระยะทาง C[a,b] ของฟังก์ชันต่อเนื่องใดๆ ที่นิยามบนช่วง [a,b] โดยมีระยะทางเพิ่มขึ้นจาก Supremum norm สมาชิกทุกตัวสามารถเขียนในรูปของลิมิตของลำดับของ ฟังก์ชันพหุนาม ได้ นี่คือเนื้อหาของ ทฤษฎีบทสโตน-ไวแยร์สตราสส์ (Stone-Weierstrass theorem)
[แก้] คุณสมบัติ
ประโยค "ลิมิตของฟังก์ชัน f ที่ p คือ L" เหมือนกับประโยค- "สำหรับลำดับลู่เข้า (xn) ใน M ซึ่งมีลิมิตเท่ากับ pลำดับ (f(xn)) ลู่เข้าสู่ลิมิต L"
ฟังก์ชัน f ต่อเนื่อง ที่ p ก็ต่อเมื่อ เราสามารถหาค่าของลิมิตของ f(x) เมื่อ x เข้าใกล้ p และค่านั้นเท่ากับ f(p) หรืออีกนัยหนึ่ง ฟังก์ชัน f แปลงลำดับใดๆ ใน M ซึ่งสู่เข้าหา p ไปเป็นลำดับ N ซึ่งลู่เข้าหา f(p)
นทางคณิตศาสตร์ ฟังก์ชันต่อเนื่อง (อังกฤษ: continuous function) คือฟังก์ชันที่ถ้าตัวแปรต้นมีค่าเปลี่ยนแปลงไปเพียงเล็กน้อย ผลลัพธ์ก็ จะมีค่าเปลี่ยนแปลงไปเพียงเล็กน้อยด้วยเช่นกัน เราเรียกฟังก์ชันที่การเปลี่ยนแปลงไปเพียงเล็กน้อยของค่าของตัวแปรต้นทำให้ เกิดการก้าวกระโดดของผลลัพธ์ของฟังก์ชันว่า ฟังก์ชันไม่ต่อเนื่อง (discontinuous function) ตัวอย่างเช่น ให้ฟังก์ชัน h(t) เป็นฟังก์ชันที่ส่งเวลา t ไปยังความสูงของต้นไม้ที่เวลานั้น เราได้ว่าฟังก์ชันนี้เป็นฟังก์ชันต่อเนื่อง อีกตัวอย่างของฟังก์ชันต่อเนื่องคือ ฟังก์ชัน T(x) ที่ส่งความสูง x ไปยังอุณหภูมิ ณ จุดที่มีความสูง x เหนือจุดพิกัดทางภูมิศาสตร์จุดหนึ่ง ในทางกลับกัน ถ้า M(t) เป็นฟังก์ชันที่ส่งเวลา t ไปยังจำนวนเงินที่อยู่ในบัญชีธนาคาร เราได้ว่า M ไม่ใช่ฟังก์ชันต่อเนื่องเนื่องจากผลลัพธ์ของฟังก์ชันมีการเปลี่ยนแปลงแบบก้าวกระโดดเมื่อมีการฝากเงินหรือถอนเงินเข้าหรือออกจากบัญชี
ในคณิตศาสตร์แขนงต่างๆ นั้นแนวคิดของความต่อเนื่องถูกดัดแปลงให้มีความเหมาะสมกับคณิตศาสตร์แขนง นั้นๆ การดัดแปลงที่พบได้บ่อยที่สุดมีอยู่ในวิชาทอพอโลยี ซึ่งท่านสามารถหาข้อมูลเพิ่งเติมได้ในบทความเรื่อง ความต่อเนื่อง (ทอพอโลยี) อนึ่ง ในทฤษฎีลำดับโดยเฉพาะในทฤษฏีโดเมน นิยามของความต่อเนื่องที่ใช้คือความต่อเนื่องของสก็อตซึ่งเป็นนิยามที่สร้างขึ้นจากความต่อเนื่องที่ถูกอธิบายในบทความนี้อีกทีหนึ่ง
ฟังก์ชันค่าจริงต่อเนื่อง
สมมติว่า f เป็นฟังก์ชันที่ส่งช่วงช่วงหนึ่งของจำนวนจริงไปยังจำนวนจริง ดังเช่นฟังก์ชัน h, T, และ M ข้างต้น ฟังก์ชันเหล่านี้สามารถเขียนแทนด้วยกราฟของฟังก์ชันบนระนาบคาร์ทีเซียน เราอาจกล่าวโดยหยาบๆ ว่าฟังก์ชัน f เป็นฟังก์ชันต่อเนื่องถ้ากราฟของฟังก์ชันเป็นเส้นที่ไม่มีจุดแหว่งหรือการ ก้าวกระโดด กล่าวคือ เราสามารถเขียนกราฟได้โดยไม่ต้องยกปากกาถ้าจะกล่าวให้รัดกุมตามหลักคณิตศาสตร์แล้ว เรากล่าวว่าฟังก์ชัน f ต่อเนื่องที่จุด c ถ้าเงื่อนไขทั้งสองข้อต่อไปนี้เป็นจริง
- ฟังก์ชัน f มีนิยามที่จุด c
- ให้ c เป็นจุดลิมิตของโดเมนของ f แล้ว ลิมิตของ f(x) เมื่อ x เข้าใกล้ c มีค่าเท่ากับ f(c)
[แก้] นิยามเอปไซลอน-เดลตา
[แก้] ตัวอย่าง
- ทุก ๆ ฟังก์ชันพหุนามเป็นฟังก์ชันต่อเนื่อง
- ทุก ๆ ฟังก์ชันตรรกยะ ฟังก์ชันเลขชี้กำลัง ลอการิธึม ฟังก์ชันรากที่ n ฟังก์ชันตรีโกณมิติ ฟังก์ชันค่าสัมบูรณ์ เป็นฟังก์ชันต่อเนื่อง (บนโดเมนที่หาค่าฟังก์ชันได้)
- ทุก ๆ ฟังก์ชันขั้นบันได เช่น ฟังก์ชันที่มีค่าเป็น 1 เมื่อ x > 0 นอกนั้นฟังก์ชันมีค่าเท่ากับ 1, เป็นฟังก์ชันไม่ต่อเนื่อง
- ฟังก์ชันดิริชเลต์ (หรือที่เรียกว่าฟังก์ชันข้าวโพดคั่ว) เป็นฟังก์ชันไม่ต่อเนื่อง
[แก้] ฟังก์ชันต่อเนื่องระหว่างปริภูมิอิงระยะทาง
[แก้] ฟังก์ชันต่อเนื่องระหว่างปริภูมิเชิงทอพอโลยี
นิยามของฟังก์ชันต่อเนื่องสามารถขยายให้กว้างขึ้น เพื่อให้ครอบคลุมฟังก์ชันระหว่างปริภูมิทอพอโลยี X,Y ได้ดังนี้: .
.อนึ่ง สามารถพิสูจน์ได้ว่าในปริภูมิยุคลิด นิยามข้างต้นและนิยามเอปไซลอน-เดลตาเหมือนกันทุกประการ. จากนิยามนี้ทำให้นักคณิตศาสตร์ทราบแก่นที่แท้จริงของความต่อเนื่องคือ การนิยามเซตเปิดในระบบนั่นเอง ไม่ใช่ฟังก์ชันระยะทางดังที่เคยเข้าใจมา
ใน คณิตศาสตร์ พหุนามอาจเป็นฟังก์ชันที่ง่ายที่สุดในการทำแคลคูลัส อนุพันธ์ และปริพันธ์เป็นไปตามกฎต่อไปนี้
บทพิสูจน์
เนื่องจากการหาอนุพันธ์เป็น การแปลงเชิงเส้น จะได้ สำหรับ จำนวนธรรมชาติ r ใดๆ ซึ่งมีการพิสูจน์โดยอุปนัย โดยใช้ กฎผลคูณ ซึ่งขึ้นอยู่กับกรณีที่ r = 1 เท่านั้น
สำหรับ จำนวนธรรมชาติ r ใดๆ ซึ่งมีการพิสูจน์โดยอุปนัย โดยใช้ กฎผลคูณ ซึ่งขึ้นอยู่กับกรณีที่ r = 1 เท่านั้น[แก้] นัยทั่วไป
นัยทั่วไปนี้ก็เป็นจริงสำหรับการหาปริพันธ์ของพนุนามเช่นเดียวกัน
ถ้ามีพนุนามที่ตัวคูณไม่ใช่จำนวนจริงหรือจำนวนเชิงซ้อน (เช่นอาจเป็น จำนวนเต็ม หรือตัวเลขมอดุโลของจำนวนเฉพาะ) ก็สามารถนิยามอนุพันธ์จากความสัมพันธ์ข้างบน
ทฤษฎีบทค่าเฉลี่ย
จากวิกิพีเดีย สารานุกรมเสรี
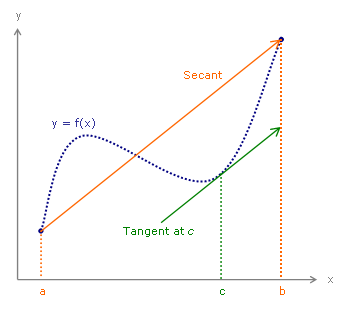
ฟังก์ชันที่มีความต่อเนื่องบนช่วง [a, b
แคลคูลัสเวกเตอร์ เป็นแขนงหนึ่งของคณิตศาสตร์ ว่าด้วยการเปลี่ยนแปลงของของเวกเตอร์ในมิติที่สูงกว่าหรือเท่ากับสองมิติ เนื้อหาประกอบด้วยเทคนิคในการแก้ปัญหา และ สูตรคำนวณที่เกี่ยวข้องต่างๆ ซึ่งมีประโยชน์ใช้งานมากในทางวิศวกรรม และ ฟิสิกส์สนามเวกเตอร์ ใช้หมายถึง การระบุค่าเวกเตอร์ให้กับทุกๆ จุดในปริภูมิที่พิจารณา เช่นเดียวกับ สนามสเกลาร์ ซึ่งเป็นการระบุค่าสเกลาร์ให้กับทุกๆ จุดในปริภูมิ เช่น อุณหภูมิของน้ำในสระ เป็นสนามสเกลาร์ โดยเป็นการระบุค่าอุณหภูมิ ซึ่งเป็นปริมาณสเกลาร์ให้กับแต่ละตำแหน่ง ส่วนการไหลของน้ำในสระนั้นเป็นสนามเวกเตอร์ เนื่องจากการไหลของน้ำที่แต่ละจุดนั้นจะถูกระบุด้วย เวกเตอร์ความเร็ว
ตัวดำเนินการที่สำคัญในแคลคูลัสเวกเตอร์:
- เกรเดียนต์ (gradient) ใช้สัญลักษณ์
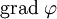 หรือ
หรือ 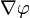 : เป็นตัวดำเนินการใช้วัดอัตรา และ ทิศทาง ความเปลี่ยนแปลงของสนามสเกลาร์ ดังนั้นเกรเดียนต์ของสนามสเกลาร์ จะได้เป็นสนามเวกเตอร์
: เป็นตัวดำเนินการใช้วัดอัตรา และ ทิศทาง ความเปลี่ยนแปลงของสนามสเกลาร์ ดังนั้นเกรเดียนต์ของสนามสเกลาร์ จะได้เป็นสนามเวกเตอร์ - ไดเวอร์เจนซ์ (divergence) ใช้สัญลักษณ์
 หรือ
หรือ 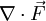 : เป็นตัวดำเนินการใช้วัด ความลู่เข้า หรือ ลู่ออก(เป็นจุดกำเนิดสนาม)ของ สนามเวกเตอร์ ณ จุดใดๆ
: เป็นตัวดำเนินการใช้วัด ความลู่เข้า หรือ ลู่ออก(เป็นจุดกำเนิดสนาม)ของ สนามเวกเตอร์ ณ จุดใดๆ - เคิร์ล (curl) ใช้สัญลักษณ์
 หรือ
หรือ 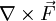 : เป็นตัวดำเนินการใช้วัดระดับความหมุนวน ณ จุดใดๆ โดย เคิร์ลของสนามเวกเตอร์ จะได้เป็นอีกสนามเวกเตอร์หนึ่ง
: เป็นตัวดำเนินการใช้วัดระดับความหมุนวน ณ จุดใดๆ โดย เคิร์ลของสนามเวกเตอร์ จะได้เป็นอีกสนามเวกเตอร์หนึ่ง
ทฤษฎีที่สำคัญที่เกี่ยวข้องกับตัวดำเนินการดังกล่าว คือ
การวิเคราะห์เหล่านี้สามารถทำความเข้าใจได้ไม่ยาก โดยการใช้วิธีการทางเรขาคณิตเชิงอนุพันธ์ (แคลคูลัสเวกเตอร์ เป็นสาขาย่อยหนึ่งของ เรขาคณิตเชิงอนุพันธ์)
ในคณิตศาสตร์ กฎผลคูณของแคลคูลัส ซึ่งเราอาจเรียกว่า กฎของไลบ์นิซ (ดูการอนุพัทธ์) ควบคุมอนุพันธ์ของผลคูณของฟังก์ชันที่หาอนุพันธ์ได้
ซึ่งอาจเขียนได้ดังนี้
ถ้าฟังก์ชันที่เราต้องการหาอนุพันธ์ f(x) สามารถเขียนในรูป
ในวิชาแคลคูลัส กฏลูกโซ่ (อังกฤษ: Chain rule) คือสูตรสำหรับการหาอนุพันธ์ของฟังก์ชันคอมโพสิต
เห็นได้ชัดว่า หากตัวแปร y เปลี่ยนแปลงตามตัวแปร u ซึ่งเปลี่ยนแปลงตามตัวแปร x แล้ว อัตราการเปลี่ยนแปลงของ y เทียบกับ x หาได้จากผลคูณ ของอัตราการเปลี่ยนแปลงของ y เทียบกับ u คูณกับ อัตราการเปลี่ยนแปลงของ u เทียบกับ x
สมมติให้คนหนึ่งปีนเขาด้วยอัตรา 0.5 กิโลเมตรต่อชั่วโมง อุณหภูมิจะ ลดต่ำลงเมื่อระดับความสูงเพิ่มขึ้น สมมติให้อัตราเป็น ลดลง 6 °F ต่อกิโลเมตร ถ้าเราคูณ 6 °F ต่อกิโลเมตรด้วย 0.5 กิโลเมตรต่อชั่วโมง จะได้ 3 °F ต่อชั่วโมง การคำนวณเช่นนี้เป็นตัวอย่างของการประยุกต์ใช้กฎลูกโซ่
ในทางพีชคณิต กฎลูกโซ่ (สำหรับตัวแปรเดียว) ระบุว่า ถ้าฟังก์ชัน f หาอนุพันธ์ได้ที่ g(x) และฟังก์ชัน g หาอนุพันธ์ได้ที่ x คือเราจะได้
 ดังนั้น
ดังนั้น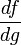 ระบุว่า f เปลี่ยนแปลงตาม g เหมือนเป็นตัวแปรหนึ่ง.
ระบุว่า f เปลี่ยนแปลงตาม g เหมือนเป็นตัวแปรหนึ่ง.ในการหาปริพันธ์ ส่วนกลับของกฎลูกโซ่คือการหาปริพันธ์โดยการแทนค่า
The general power rule
กฎเลขยกกำลังทั่วไปสามารถนำมาใช้กับกฎลูกโซ่ได้[แก้] Example I
พิจารณา f(x) = (x2 + 1)3. f(x) เทียบได้กับ h(g(x)) โดยที่ g(x) = x2 + 1 และ h(x) = x3 ดังนั้นf'(x) = 3(x2 + 1)2(2x)
= 6x(x2 + 1)2
[แก้] Example II
ในการหาอนุพันธ์ของฟังก์ชันตรีโกณมิติ- f(x) = sin(x2),
- f'(x) = 2xcos(x2)
[แก้] กฎลูกโซ่สำหรับหลายตัวแปร
กฎลูกโซ่ใช้ได้กับฟังก์ชันหลายตัวแปรเช่นกัน ตัวอย่างเช่น ถ้าเรามีฟังก์ชัน f(u(x,y),v(x,y)) โดยที่- u(x,y) = 3x + y2 และ v(x,y) = sin(xy)
[แก้] บทพิสูจน์กฎลูกโซ่
ให้ f และ g เป็นฟังก์ชัน และให้ x เป็นจำนวนที่ f สามารถหาอนุพันธ์ได้ที่ g(x) และ g หาอนุพันธ์ได้ที่ x ดังนั้น จากนิยามของการหาอนุพันธ์ได้ จะได้ ซึ่ง
ซึ่ง  ขณะที่
ขณะที่ 
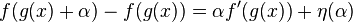 ซึ่ง
ซึ่ง  ขณะที่
ขณะที่ 
 จะเห็นว่าขณะที่
จะเห็นว่าขณะที่ 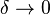 นั้น
นั้น  และ
และ 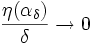 ดังนั้น
ดังนั้น ขณะที่
ขณะที่ 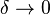
[แก้] กฎลูกโซ่พื้นฐาน
กฎลูกโซ่นั้นเป็นคุณสมบัติพื้นฐานของนิยามของอนุพันธ์ทั้งหมด เช่น ถ้า E F และ G เป็น ปริภูมิบานาค (รวมไปถึงปริภูมิยูคลิดด้วย) และ f : E → F และ g : F → G เป็นฟังก์ชัน และถ้า x เป็นสมาชิกของ E ซึ่ง f หาอนุพันธ์ได้ที่ x และ g หาอนุพันธ์ได้ที่ f(x) แล้ว อนุพันธ์ (อนุพันธ์เฟรเชต์) ของฟังก์ชันคอมโพสิต g o f ที่ x จะเป็นดังนี้การกำหนดกฎลูกโซ่ที่ชัดเจนสามารถทำได้จากวิธีที่เป็นทั่วไปมากที่สุด คือ ให้ M N และ P เป็นแมนิโฟลด์ Ck (หรือบานาคแมนิโฟลด์) และให้
- f : M → N และ g : N → P
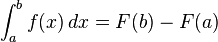



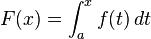




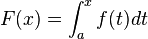

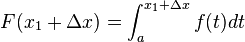


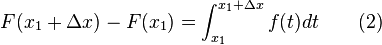
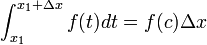





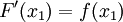


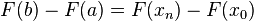
![\begin{matrix} F(b) - F(a) & = & F(x_n)\,+\,[-F(x_{n-1})\,+\,F(x_{n-1})]\,+\,\ldots\,+\,[-F(x_1) + F(x_1)]\,-\,F(x_0) \, \\
& = & [F(x_n)\,-\,F(x_{n-1})]\,+\,[F(x_{n-1})\,+\,\ldots\,-\,F(x_1)]\,+\,[F(x_1)\,-\,F(x_0)] \, \end{matrix}](http://upload.wikimedia.org/math/0/0/a/00a3846f57042fde339bf19228d95c43.png)
![F(b) - F(a) = \sum_{i=1}^n [F(x_i) - F(x_{i-1})] \qquad (1)](http://upload.wikimedia.org/math/d/2/4/d249e4e0a9d12a6df94facb0f7c99aca.png)
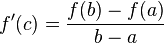

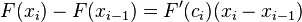
![F(b) - F(a) = \sum_{i=1}^n [F'(c_i)(x_i - x_{i-1})]](http://upload.wikimedia.org/math/2/3/3/233996a651736989a013f7a0f8be331e.png)
![F(b) - F(a) = \sum_{i=1}^n [f(c_i)(\Delta x_i)] \qquad (2)](http://upload.wikimedia.org/math/d/a/0/da0bfeefbb02affa1534e0ff44290cf7.png)
![\lim_{\| \Delta \| \to 0} F(b) - F(a) = \lim_{\| \Delta \| \to 0} \sum_{i=1}^n [f(c_i)(\Delta x_i)]\,dx](http://upload.wikimedia.org/math/1/a/7/1a7f4871055ad03967fb38b5655d3bce.png)
![F(b) - F(a) = \lim_{\| \Delta \| \to 0} \sum_{i=1}^n [f(c_i)(\Delta x_i)]](http://upload.wikimedia.org/math/f/3/2/f3271269dbb7b44389d5427dab8b09eb.png)

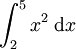

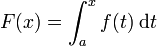

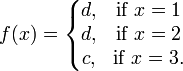

















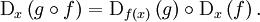
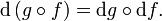
โค้ดที่เห็นเป็นโค้ดเพลงโรงเรียนนะครับ
ตอบลบ